4.1角动量及其守恒
一、质点的角动量
在我们研究旋转运动时,由于速度方向时刻发生变化,用动量来描述运动的方法不再好用。因此,物理学家们仿照动量的形式,定义出了用于描述旋转运动的角动量。
注意:角动量是由动量的概念产生的,可以算是动量在旋转运动中的特化型,其物理意义本质正是动量在转动中的表现,可以将动量与角动量类比学习!
定义:角动量 $\vec{L}=\vec{r}\times\vec{p}=\vec{r}\times m\vec{v}$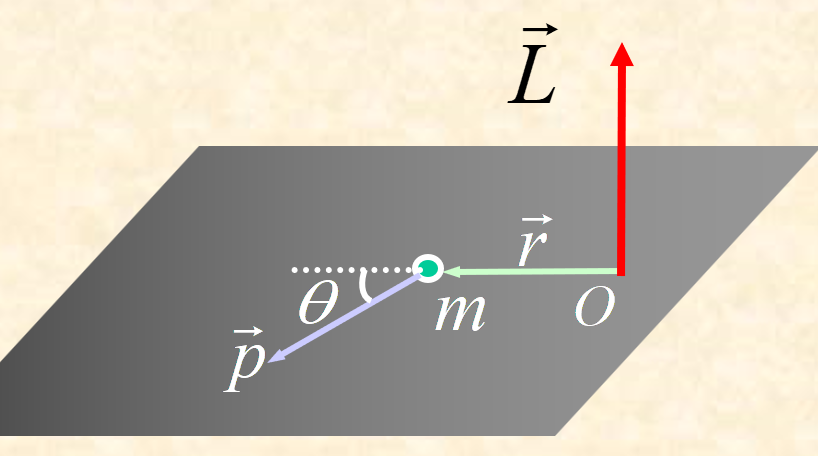
定义式中,$\vec{r}$表示从点O到质点的位置矢量,$\vec{p}$表示质点的动量。请注意:用角动量描述运动时,必须声明对应的参考点!!!
大小:$L=rp\sin\theta=mrv\sin\theta$
方向:垂直$\vec{r},\vec{p}$组成的平面 (判断:右手螺旋定则)
注意:$\vec{r}与\vec{p}$共线时,角动量为0!

二、质点的角动量定理
【复习】质点的动量定理:由牛顿第二定律$\vec{F}=\frac{\,d\vec{p}}{\,dt}$得到$\vec{F}\cdot\,dt=\,d\vec{p}$,即$\vec{I}=\vec{p_1}-\vec{p_2}$
可以看出,质点的动量定理是在研究力在时间上的累积效应,也即动量随时间的变化率。
同理,角动量定理也是在研究角动量随时间的变化率。

与动量定理类似,角动量定理将力变为力矩,动量变为角动量。力矩M效果的本质可以理解为力的作用。
三、质点的角动量守恒定律
若对某一固定点,质点所受合外力矩为零,则质点对该固定点的角动量矢量保持不变。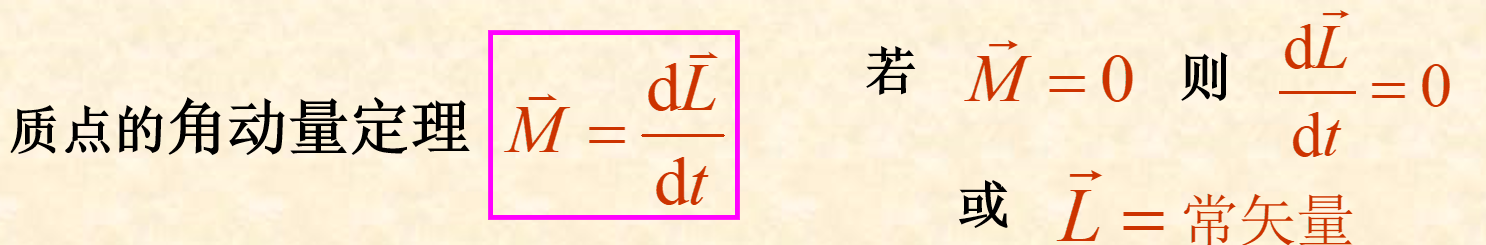
四、质点系 的角动量及角动量守恒定律
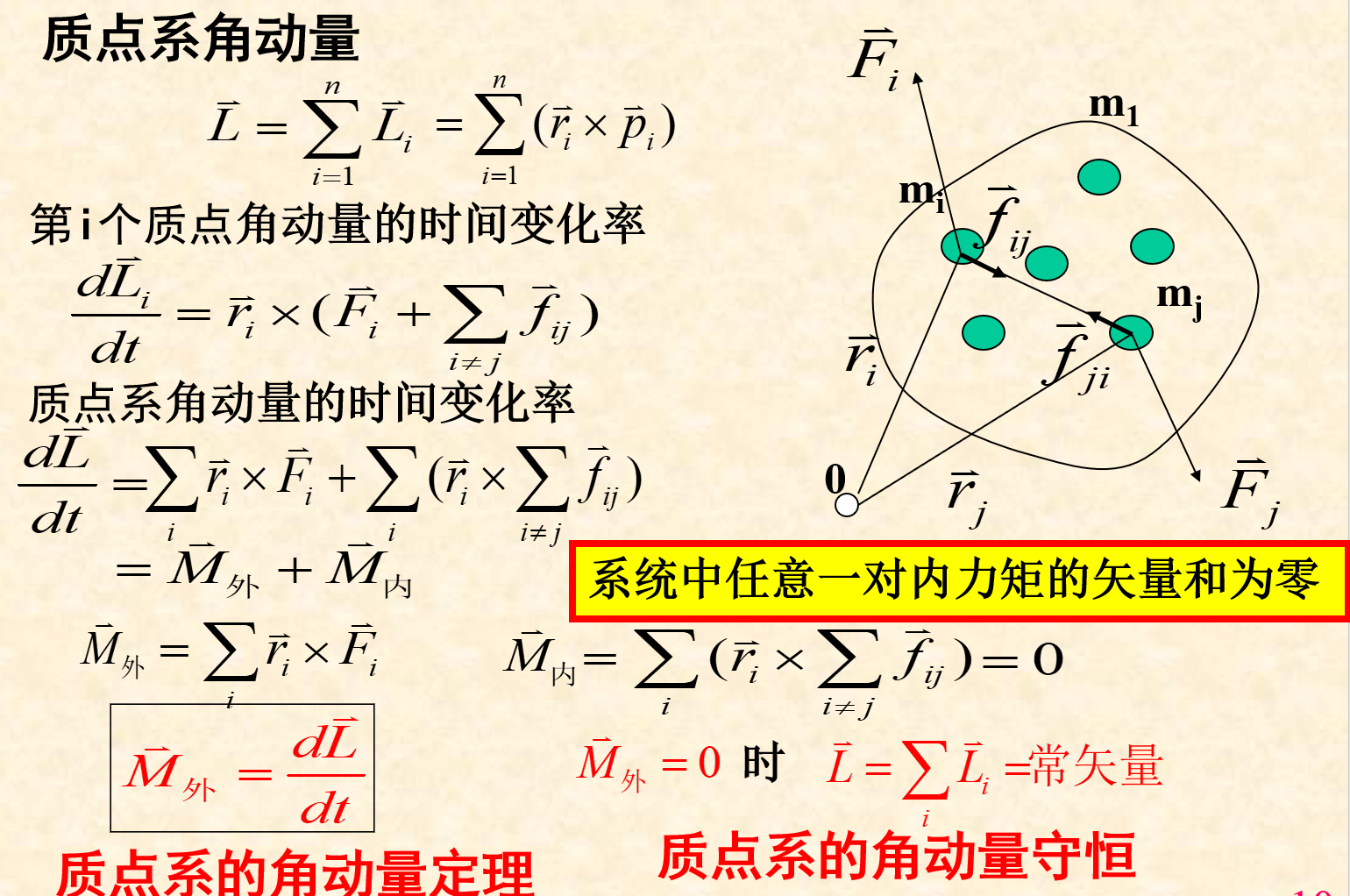
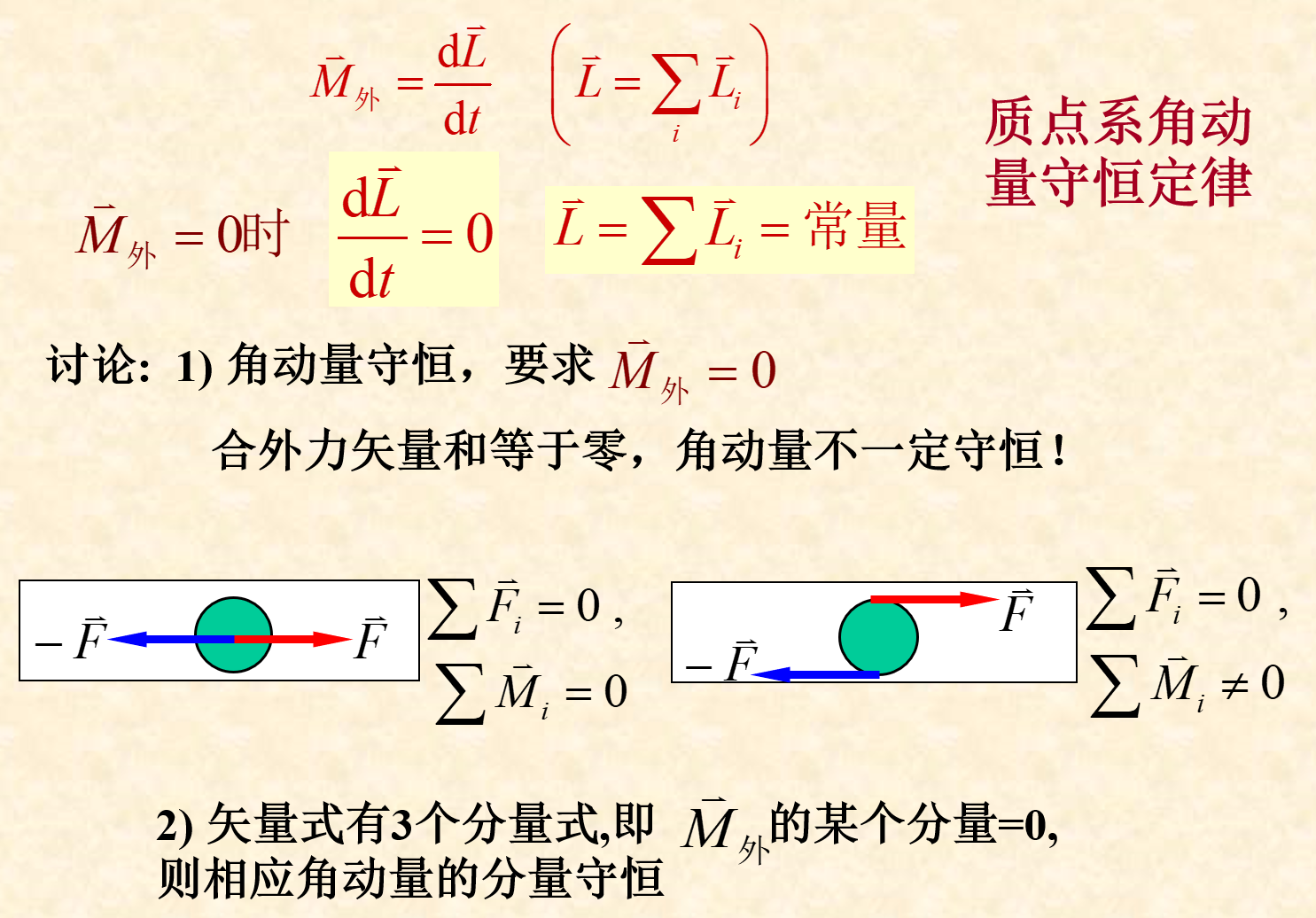
系统中任意一对内力矩的矢量和为0,所以质点系的角动量定理和角动量守恒都只和合外力矩有关。

五、质心参考系中的角动量